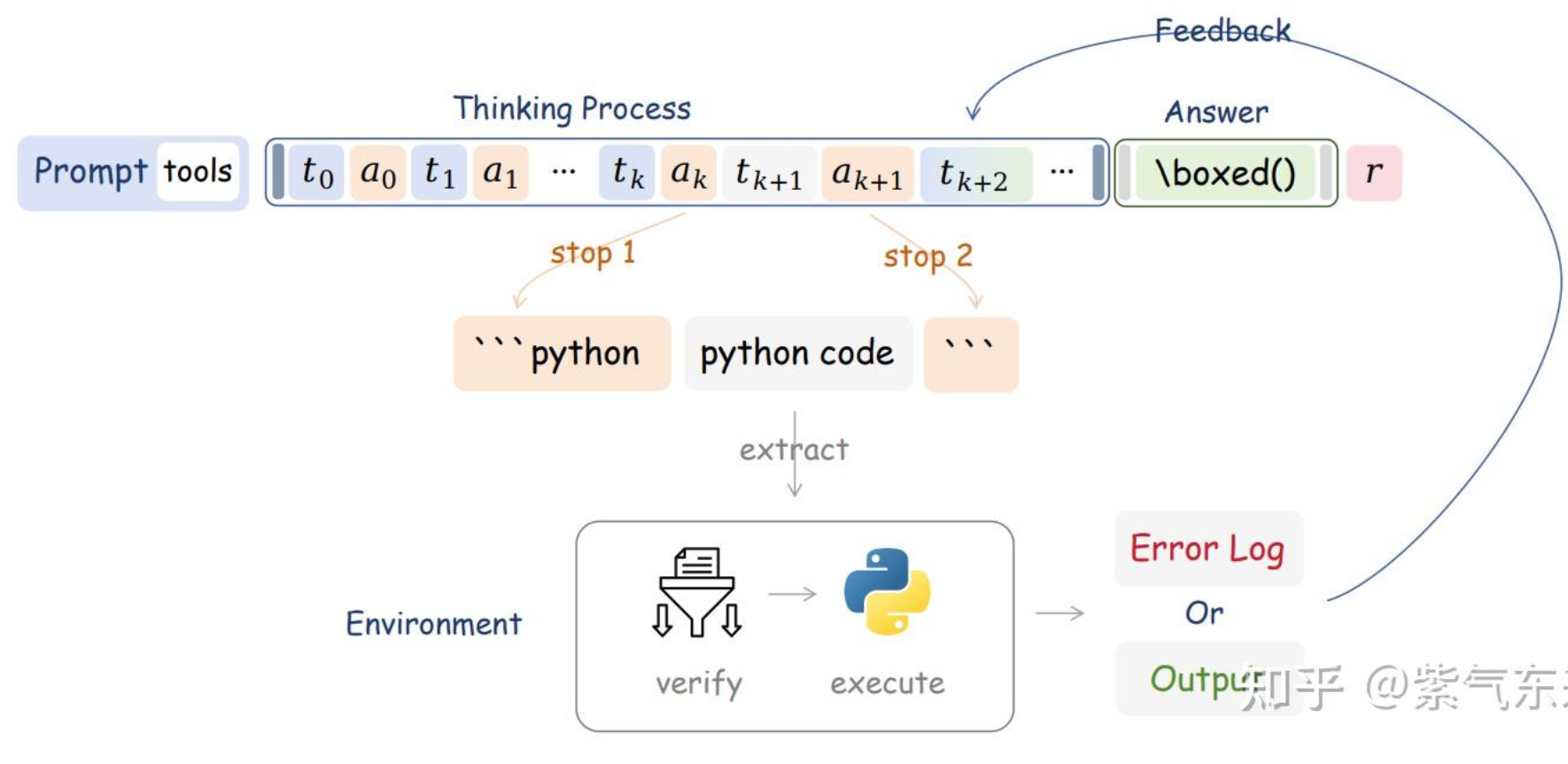
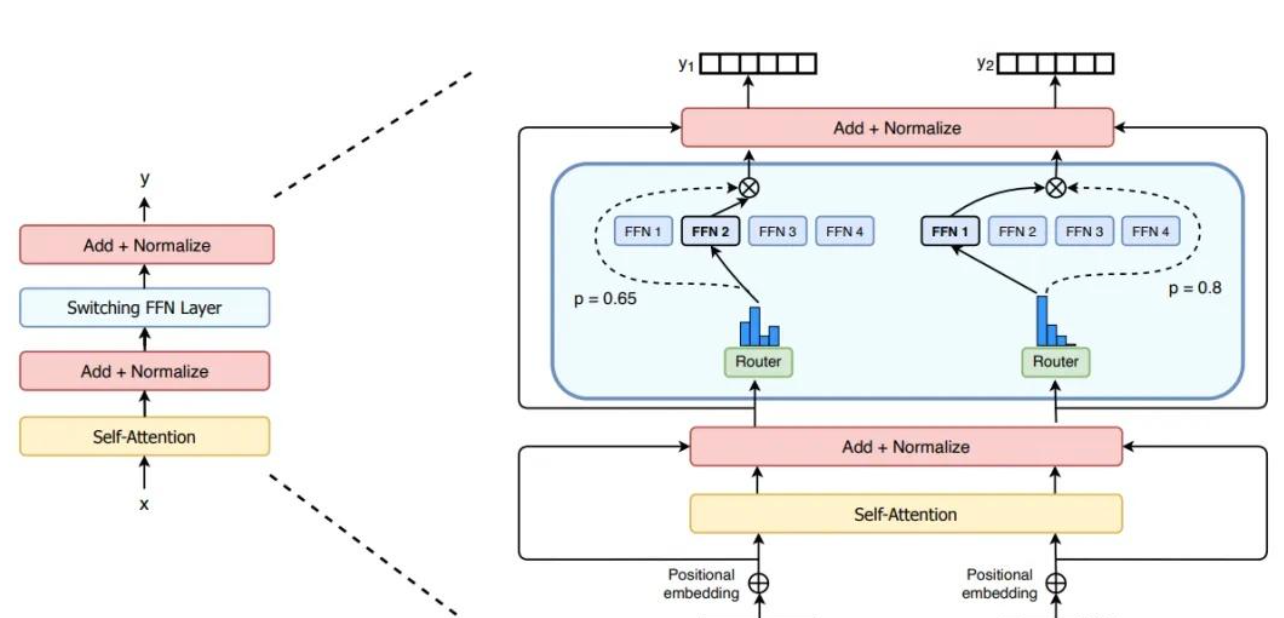
PPO：https://zhuanlan.zhihu.com/p/468828804

img

Policy Gradient公式推导与举例

1. 优化目标

我们要最大化强化学习的期望回报（Expected Return）：

Rθ=Eτ∼pθ(τ)[R(τ)]=∑τR(τ)pθ(τ){R}_\theta = \mathbb{E}_{\tau \sim p_\theta(\tau)}[R(\tau)] = \sum_\tau R(\tau) p_\theta(\tau)

  • τ\tau

    表示一条轨迹（trajectory），即从初始状态到结束的一系列

    (s1,a1,s2,a2,… )(s_1, a_1, s_2, a_2, \dots)

    。

  • pθ(τ)p_\theta(\tau)

    表示策略

    πθ\pi_\theta

    产生轨迹

    τ\tau

    的概率。

  • R(τ)R(\tau)

    是轨迹的总回报。

2. 对参数 θ\theta 求梯度

∇θRˉθ=∑τR(τ)∇θpθ(τ)\nabla_\theta \bar{R}_\theta = \sum_\tau R(\tau) \nabla_\theta p_\theta(\tau)

直接对概率 pθ(τ)p_\theta(\tau) 求导不方便。

3. 使用 log trick (对数技巧)

∇θpθ(τ)=pθ(τ)∇θlog⁡pθ(τ)\nabla_\theta p_\theta(\tau) = p_\theta(\tau) \nabla_\theta \log p_\theta(\tau)

这是右边小蓝框里的公式：

∇f(x)=f(x)∇log⁡f(x)\nabla f(x) = f(x) \nabla \log f(x)

4. 替换进目标函数

∇θRˉθ=∑τR(τ)pθ(τ)∇θlog⁡pθ(τ)\nabla_\theta \bar{R}_\theta = \sum_\tau R(\tau) p_\theta(\tau) \nabla_\theta \log p_\theta(\tau)

这一步就是图中红框标出来的地方。

5. 期望形式

上式其实是 在轨迹分布 pθ(τ)p_\theta(\tau) 下的期望：

∇θRˉθ=Eτ∼pθ(τ)[R(τ)∇θlog⁡pθ(τ)]\nabla_\theta \bar{R}_\theta = \mathbb{E}_{\tau \sim p_\theta(\tau)} [R(\tau) \nabla_\theta \log p_\theta(\tau)]

6. 蒙特卡洛近似

我们用采样得到的轨迹来估计期望：

∇θRˉθ≈1N∑n=1NR(τn)∇θlog⁡pθ(τn)\nabla_\theta \bar{R}_\theta \approx \frac{1}{N} \sum_{n=1}^N R(\tau^n) \nabla_\theta \log p_\theta(\tau^n)

其中 NN 是采样的轨迹数。

7. 分解轨迹概率

轨迹概率

θ(τ)\theta(\tau)

可以写成一连串动作选择概率的乘积：

θ(τ)=∏t=1Tπθ(at∣st)⋅P(st+1∣st,at)_\theta(\tau) = \prod_{t=1}^{T} \pi_\theta(a_t|s_t) \cdot P(s_{t+1}|s_t, a_t)

因为环境转移

P(st+1∣st,at)P(s_{t+1}|s_t, a_t)

不依赖 θ(对数求导后，环境转移与θ无关，所以这部分值被舍弃了)，所以：

∇θlog⁡pθ(τ)=∑t=1T∇θlog⁡πθ(at∣st)\nabla_\theta \log p_\theta(\tau) = \sum_{t=1}^T \nabla_\theta \log \pi_\theta(a_t|s_t)

8. 最终公式

所以得到：

∇θRˉθ≈1N∑n=1N∑t=1TnR(τn)∇θlog⁡πθ(atn∣stn)\nabla_\theta \bar{R}_\theta \approx \frac{1}{N} \sum_{n=1}^N \sum_{t=1}^{T_n} R(\tau^n) \nabla_\theta \log \pi_\theta(a_t^n | s_t^n)

这就是 REINFORCE 算法 的核心更新规则。

✅ 直观理解：

  • R(τ)R(\tau)

    ：告诉我们这条轨迹有多好。

  • ∇θlog⁡πθ(at∣st)\nabla_\theta \log \pi_\theta(a_t|s_t)

    ：告诉我们如何调整参数 θ 让动作更可能出现。

  • 两者相乘：如果回报大，就增加这条轨迹上动作的概率；如果回报小，就减少概率。

用一个非常简单的两步决策问题来举例

🎯 环境设定

  • 每条轨迹

    τ=(a1,a2)\tau = (a_1, a_2)

    ，一共两步。

  • 动作空间：{L, R}。

  • 策略：

    πθ(a∣s)\pi_\theta(a|s)

    （假设每一步状态相同，为了简单）。

  • 回报：

    • 如果轨迹是 (L, L)，回报

      R(τ)=+1R(\tau)=+1

      。

    • 其他轨迹回报

      R(τ)=0R(\tau)=0

      。

也就是说，智能体必须 连续两步选 L 才有奖励。

1. 轨迹概率

假设策略是一个伯努利分布，

  • πθ(L)=p\pi_\theta(L) = p

  • πθ(R)=1−p\pi_\theta(R) = 1-p

    。

那么轨迹概率：

  • pθ(L,L)=p⋅p=p2p_\theta(L,L) = p \cdot p = p^2

  • pθ(L,R)=p(1−p)p_\theta(L,R) = p(1-p)

  • pθ(R,L)=(1−p)pp_\theta(R,L) = (1-p)p

  • pθ(R,R)=(1−p)2p_\theta(R,R) = (1-p)^2

2. 期望回报

Rˉθ=∑τR(τ)pθ(τ)=1⋅p2+0⋅(其他)=p2\bar{R}_\theta = \sum_\tau R(\tau)p_\theta(\tau) = 1 \cdot p^2 + 0 \cdot (其他) = p^2

很直观：只有 (L,L)(L,L) 有奖励。

3. 用 log-trick 求梯度

目标函数：

∇θRˉθ=Eτ∼pθ(τ)[R(τ)∇θlog⁡pθ(τ)]\nabla_\theta \bar{R}_\theta = \mathbb{E}_{\tau \sim p_\theta(\tau)} \Big[ R(\tau)\nabla_\theta \log p_\theta(\tau)\Big]

（求和转化成期望的形式）

4. 展开公式

采样一条轨迹，比如 (L,L)，

  • 回报

    R(τ)=1R(\tau)=1

    。

  • 轨迹概率

    pθ(τ)=p2p_\theta(\tau)=p^2

    。

  • log⁡pθ(τ)=log⁡(p2)=2log⁡p\log p_\theta(\tau) = \log(p^2) = 2\log p

    。

  • ∇θlog⁡pθ(τ)=2p∇θp\nabla_\theta \log p_\theta(\tau) = \frac{2}{p} \nabla_\theta p

    。

所以：

∇θlog⁡pθ(τ)=1⋅2p∇θp\nabla_\theta \log p_\theta(\tau) = 1 \cdot \frac{2}{p} \nabla_\theta p

如果轨迹是 (R,R)，则回报 00，更新量为 00。

5. 蒙特卡洛估计

如果我们从策略中采样 N=3 条轨迹：

  • τ1=(L,L)\tau^1 = (L,L)

    ，R=1。

  • τ2=(L,R)\tau^2 = (L,R)

    ，R=0。

  • τ3=(R,L)\tau^3 = (R,L)

    ，R=0。

那么梯度估计：

∇θRˉθ≈13[1⋅∇θlog⁡p2+0+0]=13⋅2⋅1p∇θp\nabla_\theta \bar{R}_\theta \approx \frac{1}{3} \Big[ 1 \cdot \nabla_\theta \log p^2 + 0 + 0 \Big] = \frac{1}{3} \cdot 2 \cdot \frac{1}{p}\nabla_\theta p

✅ 直观解释

  • 当采样到奖励高的轨迹(L,L)）时，更新会推动 提高动作 LL 的概率。

  • 当采样到没有奖励的轨迹时，更新为 0。

  • 随着采样越来越多，估计会收敛到真实梯度

    ∇θp2\nabla_\theta p^2