LIMR解读

之前已经有很多文章研究「如何用少量精选数据提升LLM效率」这个话题了，包括之前媒体声量很大的s1和LIMO，这些工作的核心观点就是——Less is More，数据质量 > 数量。

LIMR这篇论文可以看做这种思想的延续，不过关注的点在与RL，而不是SFT。这篇论文对我来说，最有意思的点是，「如何衡量哪些数据好呢」？作者给出了一个指导思想：好的训练样本应该与模型的整体学习轨迹对齐。通俗地解释一下，这就是一种「同步进化」的思想，即高价值样本的奖励变化需要与模型能力提升同频共振。就像教学生数学，要选择那些当前稍难，但通过练习就能掌握的题目（样本A），而不是一直做简单题（样本B）或超纲题（样本C）。

实验目前做的还不是很完善，论证链条有待进一步加强。

论文与代码：GitHub - GAIR-NLP/LIMR

主要内容

1. 作者和团队信息

作者：Xuefeng Li, Haoyang Zou, Pengfei Liu。
团队：来自上海交通大学 (SJTU), 上海人工智能研究院 (SII), 通用人工智能研究院 (GAIR)。
主要贡献者：Pengfei Liu，论文通讯作者。
团队贡献：GAIR-NLP 团队在自然语言处理领域有丰富的研究成果，尤其在模型训练和优化方面。

2. 背景和动机

发表时间：2025年2月（arxiv预印版）
研究问题：如何更有效地利用强化学习（RL）训练数据，提升大型语言模型（LLM）的推理能力？
问题背景：
- 近年来，像o1、Deepseek R1、Kimi1.5等模型展示了RL在提升LLM推理能力方面的潜力。
- 然而，这些研究对于RL训练所需的数据量缺乏透明度，阻碍了进一步的研究和发展。
- 已有的开源项目在RL训练数据量上差异很大（从几千到几十万不等），缺乏明确的指导原则。
- 论文关注点：在没有数据蒸馏的情况下，直接从基座模型开始进行RL训练，类似于Deepseek R1-zero的设置。

3. 相关研究

现有研究的不足：
- 缺乏关于RL训练数据规模的明确基准，研究人员只能依赖试错，导致资源浪费和效果不佳。
- 缺乏对样本数量如何影响模型性能的系统分析，难以做出明智的资源分配决策。
- 最关键的疑问：仅仅扩大RL训练数据的规模是提升模型性能的关键吗？是否忽略了更重要的因素，如样本质量和选择标准？
对比：
- LIMO和s1：在32B参数规模的模型上，通过监督微调（SFT）在数据效率方面表现出潜力。但本文发现，在7B参数规模的模型上，这些方法表现不佳。

4. 核心思路

核心观点：训练样本的质量和相关性远比数量重要。
主要思路：
- 通过实验观察：发现精心挑选的RL训练样本子集（1,389个）可以达到甚至超过使用完整数据集（8,523个）的性能。
- 提出Learning Impact Measurement (LIM)：一种自动化的定量方法，用于评估RL训练样本的潜在价值，预测哪些样本对模型改进贡献最大。

5. 方案与技术

Learning Impact Measurement (LIM)：
- 模型对齐的轨迹分析：基于样本对模型学习的贡献来评估训练样本。
- 关键发现：学习模式与模型整体性能轨迹互补的样本更有价值。
- 计算方法：
  - 首先使用模型平均奖励曲线作为参考：
    其中表示第个样本在第个 epoch 的奖励，是样本总数。
  - 然后计算每个样本的归一化对齐分数（normalized alignment score）：，这个公式衡量了样本学习模式与模型整体学习轨迹的对齐程度，分数越高表示对齐越好。
- 样本选择策略：选择分数高于阈值的样本：。实验中，时，从原始数据集中选择了1,389个高质量样本，组成了LIMR数据集。
基线方法：
- 随机抽样 (RAND)：从MATH-FULL数据集中随机选择1,389个样本，作为对比的基准。
- 线性进度分析 (LINEAR)：根据样本在训练 epochs 中显示出稳定改进的一致性来评估样本。
奖励设计：
- 与Deepseek R1类似，使用基于规则的奖励函数。
  - 答案正确：奖励为1。
  - 答案不正确但格式正确：奖励为-0.5。
  - 答案格式错误：奖励为-1。
- 公式：

6. 实验与结论

实验设置：
- 训练：使用OpenRLHF框架中实现的PPO算法。
  - 初始策略模型：Qwen2.5-Math-7B。
  - Rollout batch size：1,024，每个 prompt 生成8个样本（温度为1.2）。
  - 训练 batch size：256。
  - Actor 和 Critic 模型的学习率分别为 5e-7 和 9e-6，KL 系数为 0.01。
- 评估：在多个 benchmark 上进行评估。
  - MATH500
  - AIME2024
  - AMC2023
  - 使用 vLLM 框架加速评估过程。
  - 对于 AIME24 和 AMC23，每个问题进行4次抽样（温度为0.4）。对于 MATH500，采用贪婪解码进行推理。
主要结果：
- 直接对 Qwen-Math-7B 应用 RL，使用 MATH-FULL 数据集可以显著提高性能。
- 不同的数据选择策略导致性能差异。
  - 与完整数据集相比，使用 MATH-RAND 数据集导致平均准确率下降 8.1%。
  - MATH-LINEAR 仅导致 2% 的损失。
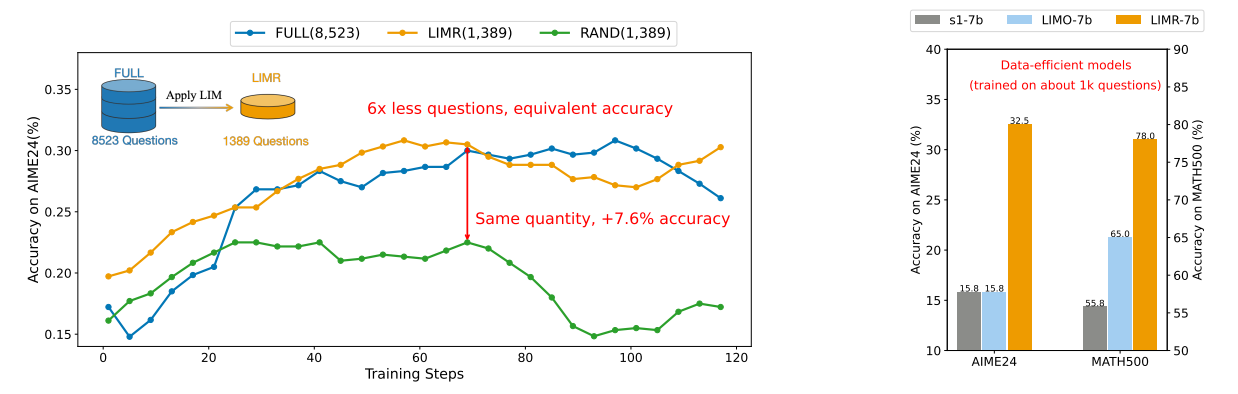
  - LIMR 仅使用了 8,523 个样本中的 1,389 个，但性能与 MATH-FULL 几乎相当。
- LIMR 和 MATH-FULL 的准确率曲线几乎相同，都明显优于 MATH-RAND。
- MATH-FULL 的训练曲线在序列长度方面表现出不稳定性，而 LIMR 的相应曲线先下降后逐渐上升。
- LIMR 的奖励曲线上升更快，并最终接近 1.0，表明模型有效地利用了 LIMR 数据集进行学习。
- 在相同的数据量下，RL 比 SFT 更有效。与 LIMO 和 s1 相比，LIMR 在 AIME 上的相对改进超过 100%，在 AMC23 和 MATH500 上的准确率至少提高了 10%。

7. 贡献

对后续研究的启发和影响：
- 挑战了传统观点，即扩大 RL 训练数据对于提升 LLM 推理能力是必要的。
- LIM 方法为研究人员提供了一种可扩展的解决方案，以实现高效的 RL 训练。
- 强调了优化样本质量而非增加数据数量的重要性。
- 结合高效数据选择的 RL 对于数据有限的小型模型可能特别有效。
未来潜在的可能性和启发：
- LIM 方法可以应用于其他领域，而不仅仅是数学推理。

8. 不足

LIM 方法的局限性：
- LIM 依赖于奖励函数的设计，如果奖励函数不能准确反映模型的学习效果，LIM 的效果可能会受到影响。
- LIM 的计算复杂度较高，需要对每个样本进行多次评估，计算资源消耗较大。
- 阈值的选择可能会影响 LIM 的效果，需要根据具体情况进行调整。
实验设置的局限性：
- 实验仅使用了 Qwen-Math-7B 模型，LIMR 方法在其他模型上的效果如何尚不清楚。
- 实验仅在数学推理任务上进行了评估，LIMR 方法在其他任务上的效果如何尚不清楚。

QA

Q1：为什么作者认为应该关注于没有经过蒸馏的基座模型？

因为作者想研究最原始的RL scaling 规律，如果使用蒸馏模型，会引入额外的偏差，影响研究结果的准确性。
Deepseek R1-zero 也是从零开始，没有使用任何蒸馏数据，这与本文的研究目标一致。

Q2：LIM 方法的核心思想是什么？它是如何衡量样本价值的？

LIM 的核心思想是：好的训练样本应该与模型的整体学习轨迹对齐。
具体来说，LIM 假设神经网络的学习过程通常遵循对数增长模式。因此，它使用模型的平均奖励曲线作为参考，来衡量每个样本的学习模式与整体学习轨迹的对齐程度。
如果一个样本的学习模式与模型的整体学习轨迹相似，那么它就被认为更有价值。

Q3：归一化对齐分数是如何计算的？它代表什么含义？

具体来说，它首先计算样本在每个 epoch的奖励与该样本的平均奖励之间的差异，以及模型在每个 epoch的平均奖励与整体平均奖励之间的差异。
然后，它将这两个差异向量进行点积，并除以它们的模长的乘积，得到余弦相似度。
余弦相似度的取值范围在 -1 到 1 之间。
- 值越接近 1，表示样本的学习轨迹与模型平均学习轨迹越相似，即该样本对模型的学习贡献越大。
- 值越接近 -1，表示样本的学习轨迹与模型平均学习轨迹越相反，即该样本对模型的学习可能产生负面影响。
- 值接近 0，表示样本的学习轨迹与模型平均学习轨迹不相关。

Q4：为什么在 AIME24 和 AMC23 上要进行多次抽样，而在 MATH500 上采用贪婪解码？

AIME24 和 AMC23 的问题数量较少（分别为30和40），为了更准确地评估模型在这两个 benchmark 上的性能，作者采用了多次抽样的方法，即对每个问题进行多次推理，然后取平均结果。这样可以减少随机性带来的影响。
MATH500 的问题数量较多（500），为了加快评估速度，作者采用了贪婪解码的方法，即每次选择概率最高的 token 作为输出。

Q5：如何理解「RL outperforms SFT in Data Efficiency」这一结论？

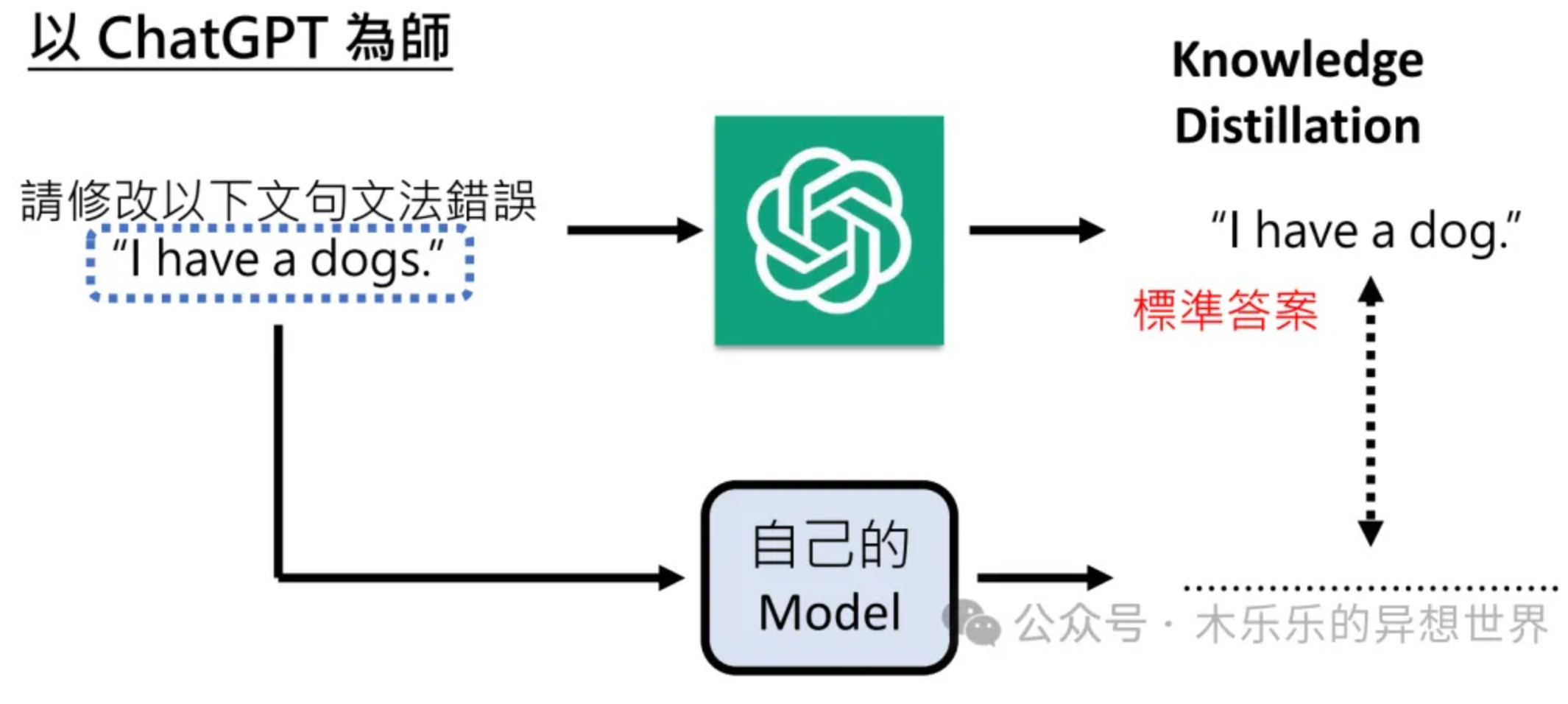
LIMO 和 s1 等工作表明，通过蒸馏等方式，可以利用少量数据来提升模型的推理能力。
但是，本文的实验结果表明，在数据量有限的情况下，使用 RL 方法比使用 SFT 方法更有效。
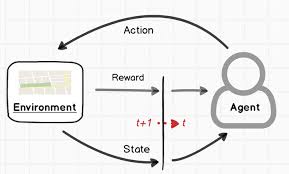
这可能是因为 RL 方法可以通过与环境的交互来学习，从而更好地利用有限的数据。而 SFT 方法只能通过模仿来学习，对数据的依赖性更强。
因此，对于小型模型来说，RL 可能是更有效的数据利用方式。

PPO的探索特性可能是关键因素：

探索-利用平衡：PPO在训练时生成多个候选答案（文中设置8个样本/prompt），通过优势函数筛选高质量轨迹。这种机制允许模型发现超出原始数据分布的解决方案。
隐式数据增强：每次迭代中，模型实际接触的数据量是原始数据量的数倍（8倍于batch size），相当于自动扩展了训练集。
对比验证：若在SFT中引入相似的数据增强（如对同一问题生成多个答案并选择最优），可能缩小与RL的差距。
核心差异：RL通过环境交互实现动态课程学习，而SFT是静态知识注入。

Q6：LIMR 方法有哪些潜在的应用场景？

节省计算资源：LIMR 可以通过选择高质量的训练样本来减少数据量，从而降低训练成本，节省计算资源。
提升小模型的性能：LIMR 结合 RL 方法，可以更有效地利用有限的数据，从而提升小模型的性能。
加速模型开发：LIMR 可以帮助研究人员更快地找到有价值的训练样本，从而加速模型开发过程。
应用于其他领域：LIMR 的思想可以应用于其他领域，例如图像识别、语音识别等，通过选择高质量的训练样本来提升模型性能。

Q7：LIM方法的核心假设是「样本学习轨迹与模型整体轨迹的对齐性决定其价值」。这一假设是否忽视了样本间的协同效应？

LIM方法确实可能忽略样本间的协同效应。当前的评分机制基于个体样本的轨迹相关性，未考虑样本组合对模型学习的互补性。例如，某些在早期阶段表现平平的样本可能在后期与其他样本结合时触发关键推理能力的突破。

潜在风险：单纯选择高LIM分数的样本可能导致训练数据同质化，削弱模型处理多样化问题的能力。
改进方向：可引入群体智能（swarm intelligence）思想，设计基于样本集的动态评分机制，评估样本组合的整体价值。例如，使用强化学习优化样本子集的组合策略，而不仅是个体分数。

Q8：论文强调在7B模型上RL优于SFT，但这是否源于SFT数据选择策略的次优性？LIMO和s1的数据是否真正适合7B模型的容量？

作者的结论可能受限于对比实验设计：

数据适配性问题：LIMO和s1的数据可能针对更大模型（如32B）优化，直接用于7B模型可能导致知识蒸馏失效。例如，复杂的长链推理数据可能超出小模型的学习能力。
训练策略差异：SFT通常需要更精细的学习率调度和数据增强，而论文未说明是否对SFT进行了充分优化。
验证方法：需控制变量实验，例如：
- 使用相同数据分别进行RL和SFT训练，比较结果。
- 调整SFT训练参数（如学习率、批大小）以适配小模型。
深层启示：模型规模与数据复杂度需匹配，盲目采用大模型数据可能损害小模型性能。

Q9：LIM的样本选择基于静态阈值θ=0.6，是否应动态调整以适配不同训练阶段？

固定阈值的局限性明显：

阶段适应性缺失：模型在不同训练阶段需要不同难度的样本。早期可能需要高奖励样本建立基础能力，后期则需要挑战性样本突破瓶颈。
数据分布偏移风险：随着模型能力提升，原高价值样本可能逐渐失效（如模型已完全掌握），但静态选择机制无法及时淘汰过时样本。
改进思路：
- 设计自适应阈值机制，例如基于模型当前平均奖励动态调整θ。
- 引入课程学习（curriculum learning），分阶段调整样本选择策略。例如，早期选择高LIM分数样本，后期逐步加入低分数但高多样性的样本。

Q10：实验仅验证数学推理任务，LIM方法是否受限于任务特性？例如，在需要常识推理或创造性生成的任务中，轨迹对齐假设是否依然成立？

任务特性可能显著影响LIM的有效性：

数学推理的确定性：数学问题通常有明确答案，奖励函数容易设计，而开放性任务（如创意写作）的奖励更模糊，可能削弱LIM的评估准确性。
学习轨迹的可预测性：数学问题的解决过程往往呈现清晰的渐进模式（如从简单算术到复杂证明），而创造性任务的学习轨迹可能更加非线性。
验证必要性：需在多样化任务（如代码生成、故事创作）中测试LIM的泛化性。
潜在挑战：
- 如何定义非确定性任务的奖励函数？
- 如何量化开放性任务的“学习轨迹”？

Q11：LIMR声称无需蒸馏，但实验中使用的Qwen-Math-7B基座模型是否已隐含数学能力？该基座模型是否经过数学相关预训练，导致结论难以推广到纯通用基座模型？

模型的预训练数据可能影响结论普适性：

Qwen-Math-7B的特性：根据技术报告，该模型已在数学语料上进行继续预训练，并非纯通用基座模型。这意味着LIMR的效果可能部分源于基座模型的数学偏向性。
泛化性风险：若换用通用基座模型（如Llama-3），可能需要更大量数据才能达到相同效果，导致LIMR的相对优势减弱。
验证建议：补充实验对比不同基座模型（数学专用 vs 通用）下的LIMR效果差异。

伪代码

下面是一个极简的伪代码流程演示，原版代码可以直接去项目里看。

import torch
import torch.nn as nn
from torch.utils.data import Dataset, DataLoader
import numpy as np
from collections import defaultdict

# 假设的数学问题数据集（需替换为真实数据）
class MathDataset(Dataset):
    def __init__(self):
        self.questions = [
            {"id": 0, "text": "解方程 x^2 + 2x + 1 = 0", "difficulty": 3},
            {"id": 1, "text": "求导数 d/dx(sin(x))", "difficulty": 2},
            # … 添加更多样本
        ]
        
    def __len__(self):
        return len(self.questions)
    
    def __getitem__(self, idx):
        return self.questions[idx]

# 基于Transformer的Actor-Critic模型
class MathSolver(nn.Module):
    def __init__(self, vocab_size=10000, embed_dim=256):
        super().__init__()
        self.embedding = nn.Embedding(vocab_size, embed_dim)
        self.transformer = nn.TransformerEncoder(
            nn.TransformerEncoderLayer(d_model=embed_dim, nhead=8),
            num_layers=6
        )
        self.actor = nn.Linear(embed_dim, vocab_size)  # 生成答案
        self.critic = nn.Linear(embed_dim, 1)         # 评估状态价值

    def forward(self, input_ids):
        embeds = self.embedding(input_ids)
        hidden = self.transformer(embeds)
        logits = self.actor(hidden[:, -1, :])  # 取最后一个token的表示
        value = self.critic(hidden[:, -1, :])
        return logits, value

# 实现LIM的核心计算
class LIMCalculator:
    def __init__(self):
        self.sample_rewards = defaultdict(list)  # {样本ID: [epoch1奖励, epoch2奖励…]}
        self.avg_rewards = []                    # 每个epoch的平均奖励

    def update(self, epoch, sample_ids, rewards):
        """记录每个样本的奖励历史"""
        for sid, r in zip(sample_ids, rewards):
            self.sample_rewards[sid].append(r)
        self.avg_rewards.append(np.mean(rewards))

    def compute_lim_scores(self):
        """计算LIM分数（与平均奖励轨迹的余弦相似度）"""
        scores = {}
        K = len(self.avg_rewards)  # 总训练轮次
        
        # 转换为张量便于计算
        avg_tensor = torch.tensor(self.avg_rewards)
        avg_mean = torch.mean(avg_tensor)
        
        for sid in self.sample_rewards:
            # 对齐历史长度（处理部分样本未参与早期训练的情况）
            sample_r = self.sample_rewards[sid]
            if len(sample_r) < K:
                sample_r = [0.0]*(K - len(sample_r)) + sample_r
                
            sample_tensor = torch.tensor(sample_r)
            sample_mean = torch.mean(sample_tensor)
            
            # 计算协方差
            numerator = torch.sum((sample_tensor - sample_mean) * (avg_tensor - avg_mean))
            denominator = torch.sqrt(
                torch.sum((sample_tensor - sample_mean)**2) * 
                torch.sum((avg_tensor - avg_mean)**2)
            ) + 1e-8  # 防止除零
            
            scores[sid] = (numerator / denominator).item()
        return scores

# 强化学习训练流程
def train_limr():
    # 初始化
    device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
    dataset = MathDataset()
    model = MathSolver().to(device)
    optimizer = torch.optim.AdamW(model.parameters(), lr=5e-5)
    lim_calculator = LIMCalculator()
    
    # 训练参数
    num_epochs = 10
    batch_size = 32
    gamma = 0.99       # 折扣因子
    clip_epsilon = 0.2 # PPO裁剪系数
    
    for epoch in range(num_epochs):
        dataloader = DataLoader(dataset, batch_size=batch_size, shuffle=True)
        epoch_rewards = []
        
        for batch in dataloader:
            # 生成答案（假设已转换为token id）
            input_ids = … # 实际需要文本编码处理
            old_logits, old_values = model(input_ids)
            
            # 使用当前策略采样多个答案（PPO中的rollout）
            with torch.no_grad():
                new_logits, new_values = model(input_ids)
                action_probs = torch.softmax(new_logits, dim=-1)
                actions = torch.multinomial(action_probs, num_samples=8)  # 每个问题生成8个答案
            
            # 计算奖励（示例规则）
            rewards = []
            for qid, action in zip(batch['id'], actions):
                # 此处应实现答案验证逻辑，示例使用随机值
                if np.random.rand() > 0.7:   # 30%正确率
                    reward = 1.0
                elif np.random.rand() > 0.3: # 40%格式正确但答案错误
                    reward = -0.5
                else:                        # 30%格式错误
                    reward = -1.0
                rewards.append(reward)
            rewards = torch.tensor(rewards).to(device)
            
            # 记录LIM数据
            lim_calculator.update(epoch, batch['id'], rewards.cpu().numpy())
            
            # PPO更新计算（简化版）
            # 计算新旧策略概率比
            new_probs = torch.log_softmax(new_logits, dim=-1)
            old_probs = torch.log_softmax(old_logits.detach(), dim=-1)
            ratio = torch.exp(new_probs - old_probs)
            
            # 计算优势函数
            advantages = rewards - old_values.squeeze()
            
            # PPO损失计算
            surr1 = ratio * advantages
            surr2 = torch.clamp(ratio, 1-clip_epsilon, 1+clip_epsilon) * advantages
            actor_loss = -torch.min(surr1, surr2).mean()
            
            critic_loss = nn.MSELoss()(new_values.squeeze(), rewards)
            
            # 反向传播
            loss = actor_loss + 0.5 * critic_loss
            optimizer.zero_grad()
            loss.backward()
            optimizer.step()
        
        # 每轮结束后计算LIM分数并筛选样本
        if epoch % 2 == 0:  # 每2轮筛选一次
            lim_scores = lim_calculator.compute_lim_scores()
            top_samples = sorted(lim_scores.items(), key=lambda x: x[1], reverse=True)[:500]
            # 更新数据集为高LIM分数样本（此处需实现数据集动态更新逻辑）
            
# 运行训练
if __name__ == "__main__":
    train_limr()