极简 Megatron-LM 模型并行切分介绍

转自：https://zhuanlan.zhihu.com/p/498422407

在大模型流行的年代，我经常需要给同事解释 Megatron-LM 是怎么做的模型并行，自己也经常记不清从头推。而现有大多数的文章都是算法向或者历史向的，信息浓度比较低。为了节省大家的时间，在这里记录一下 Megatron-LM 的切分方式。由于只考虑切分，所以本文忽略 transformer 模型中的各种 elementwise 运算和 layernorm。

下文中，我们规定 b 为 batch size，s 为 sequence length，h 为 hidden size，n 为 num head，p 为切分数，用中括号表示 tensor 形状，例如 [b, s, h] 为常规的 transformer encoder 输入。这种表示方法参考了尤洋老师的 An Efficient 2D Method for Training Super-Large Deep Learning Models。

transformer encoder 结构

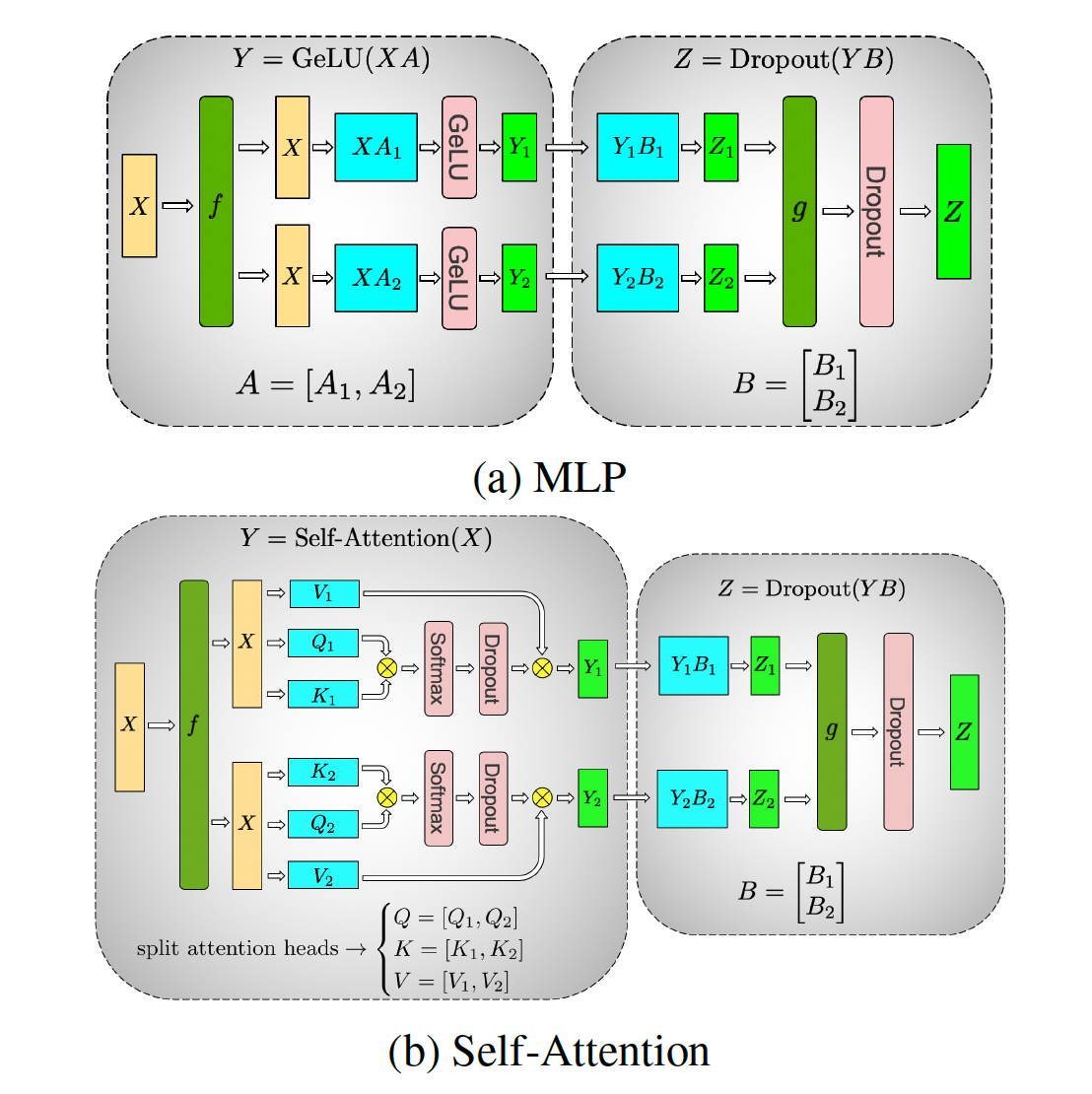
transformer encoder 由两部分组成，self attention 和 mlp。

self attention 的计算是这样的：

  1. [b, s, h] x [h, 3h] = [b, s, 3h]
  2. [b, s, 3h] 从最后一维被分为 3 组，被称为 Q, K, V，每组是 n 个 [b, s, h/n]
  3. Q、K 两组对应的项做乘法，也就是 n 个 [b, s, h/n] x [b, s, h/n]^T = [b, s, h/n] x [b, h/n, s] = [b, s, s]
  4. 得到的 n 个 [b, s, s] 和对应的 V 做乘法，得到 n 个 [b, s, s] x [b, s, h/n] = [b, s, h/n]
  5. n 个 [b, s, h/n] concat 到一起，得到 [b, s, h]
  6. [b, s, h] x [h, h] = [b, s, h]

注意 self attension 中的参数为 1 中的 [h, 3h] 和 6 中的 [h, h]，其他均为 activation。

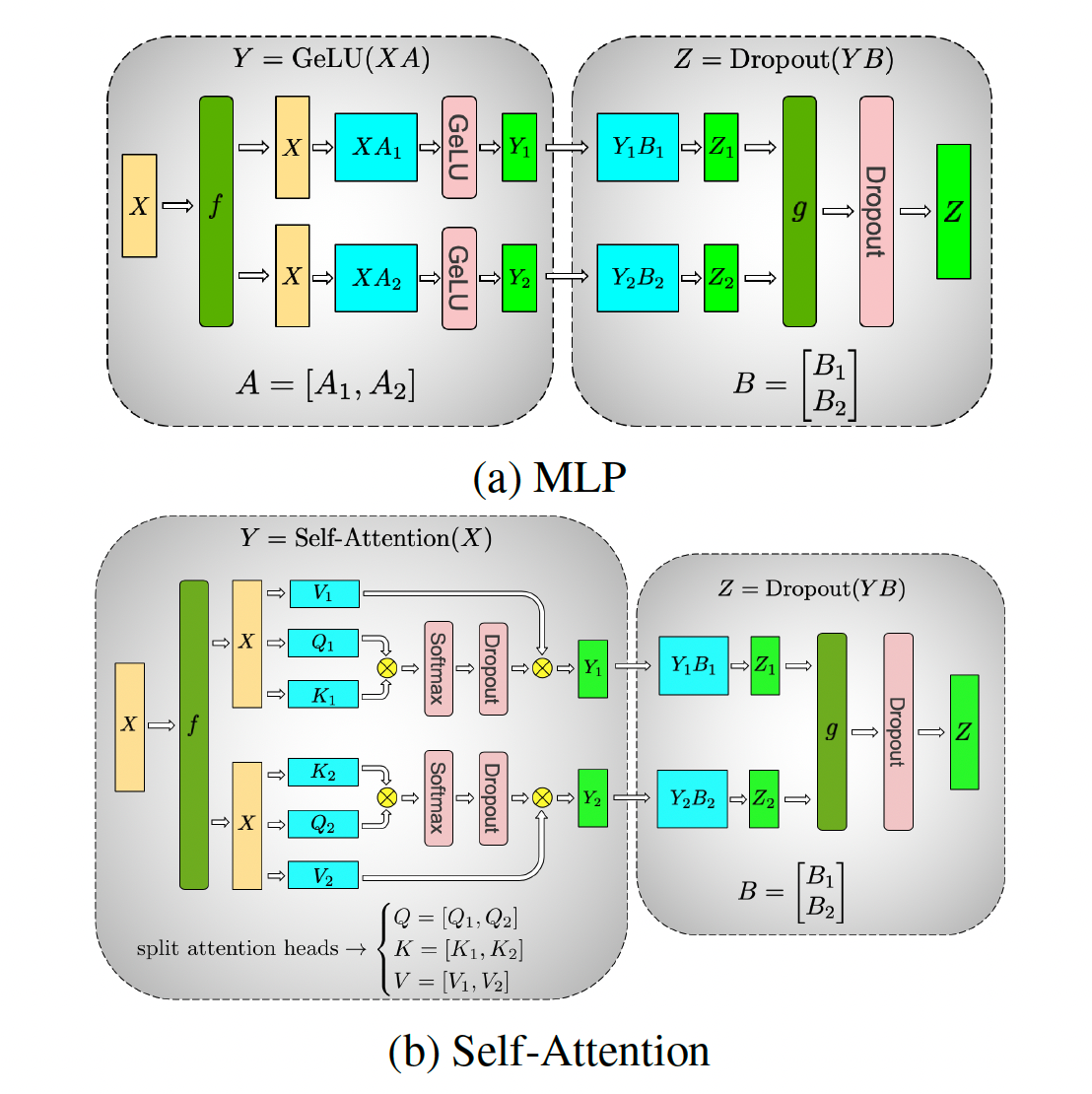
mlp 的计算是这样的：

  1. [b, s, h] x [h, 4h] = [b, s, 4h]
  2. [b, s, 4h] x [4h, h] = [b, s, h]

mlp 中参数为 [h, 4h] 和 [4h, h]。

Megatron-LM 切分

注意 Megatron-LM 切分了所有的参数。

self attention 中，将 [h, 3h] 切分成了 [h, 3h/p]，把 [h, h] 切分成了 [h/p, h]，从而使得计算步骤变为：

  1. [b, s, h] x [h, 3h/p] = [b, s, 3h/p]
  2. [b, s, 3h/p] 被分为 3 组，每组 n/p 个 [b, s, h/n]
  3. Q、K 两组对应的项做乘法，也就是 n/p 个 [b, s, h/n] x [b, s, h/n]^T = [b, s, h/n] x [b, h/n, s] = [b, s, s]
  4. 得到的 n/p 个 [b, s, s] 和对应的 V 做乘法，得到 n/p 个 [b, s, s] x [b, s, h/n] = [b, s, h/n]
  5. n/p 个 [b, s, h/n] concat 到一起，得到 [b, s, h/p]
  6. [b, s, h/p] x [h/p, h] = [b, s, h]
  7. 注意这时每张卡上都有一份 [b, s, h]，需要对这 p 个 [b, s, h] 做一次 allreduce 得到最终的 [b, s, h]

mlp 中，将 [h, 4h] 切分成了 [h, 4h/p]，把 [4h, h] 切分成了 [4h/p, h]，从而使计算步骤变为：

  1. [b, s, h] x [h, 4h/p] = [b, s, 4h/p]
  2. [b, s, 4h/p] x [4h/p, h] = [b, s, h]
  3. 类似 self attention，这时有 p 个 [b, s, h]，需要做一次 allreduce 得到最终的 [b, s, h]

为什么等价

主要要清楚两个基本的分块矩阵乘法：

1
2
3
4
5
| A1 |        |A1 x B|
| A2 |  x B = |A2 x B|

           |B1|
|A1, A2| x |B2| = A1 x B1 + A2 x B2

以及注意到 self attention 中的 Q, K, V 每一条的内部是没有进行切分的，所以可以理解为只是纵向切分了他们的计算结果，即可。

img

反向的重点是 tp 并不是每张卡一个单独的计算图（如上图），而是所有卡合成一个计算图，相当于是 tp_rank 张卡只做 1 次 backward，而不是像 dp 那样每张卡都做 backward，所以在考虑 tp 的反向的时候，可以把他们连到一张卡上，这样：

  • 上图 f 的部分，相当于 X 有 2 个分支，反向的时候两个分支的梯度要求和，也就是 f 处反向要做一次 allreduce；
  • 上图 g 的部分，相当于是求和，那么反向就是 identity。