饱和（saturating）和非饱和（non-saturating）的激活函数

在神经网络中，激活函数是决定网络能否学习复杂模式的关键因素之一。激活函数的选择会影响网络的收敛速度、性能以及最终的泛化能力。激活函数可以根据其输出特性被分为“饱和”（saturating）和“非饱和”（non-saturating）两大类：

饱和激活函数（Saturating Activation Functions）

定义：
- 饱和激活函数是指当输入值增大或减小时，函数的输出值会达到一个上限或下限，并在该范围内趋于稳定，不再随输入的增加而显著变化。
特点：
- 输出值存在一个明显的上限和下限。
- 当输入值增大到一定程度后，输出值不再显著增加（或减少）。
例子：
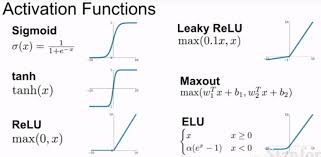
- Sigmoid 函数：[ \sigma(x) = \frac{1}{1 + e^{-x}} ]
- Tanh 函数（双曲正切函数）：[ \tanh(x) = \frac{2}{1 + e^{-2x}} - 1 ]
- ReLU 函数（Rectified Linear Unit）在正区间内是非饱和的，但在负区间内是饱和的。
影响：
- 饱和激活函数容易导致梯度消失问题，特别是在深层网络中，因为当输入值远离激活函数的线性区域时，梯度会非常小。

非饱和激活函数（Non-saturating Activation Functions）

定义：
- 非饱和激活函数是指无论输入值如何变化，函数的输出值和梯度都不会趋于一个固定的上限或下限。
特点：
- 输出值和梯度随输入值的增加而持续增加或减少，没有明显的饱和点。
例子：
- ReLU 函数（Rectified Linear Unit）：[ \text{ReLU}(x) = \max(0, x) ]
- Leaky ReLU：[ \text{LeakyReLU}(x) = \max(0.01x, x) ]
- Parametric ReLU (PReLU) 和其他变种。
影响：
- 非饱和激活函数有助于缓解梯度消失问题，因为它们在整个输入范围内都能保持较大的梯度。
- 但是，ReLU等激活函数可能会导致梯度爆炸问题，特别是在训练初期或输入值较大时。

在实际应用中，选择哪种类型的激活函数取决于具体的任务、网络结构以及训练策略。例如，ReLU及其变种由于计算简单且能有效缓解梯度消失问题，因此在许多现代深度学习模型中被广泛使用。然而，在某些情况下，如输出需要被限制在特定范围内或需要输出概率分布时，饱和激活函数（如Sigmoid或Softmax）可能更为合适。