残差连接（Residual Connection）

【深度学习 | ResNet核心思想】残差连接 & 跳跃连接：让信息自由流动的神奇之道-CSDN博客

image-20240909210607856.png

背景：

在深度神经网络中，随着层数的增加，网络的性能在一定程度上会提高（网格退化 Degradation）。然而，深度网络的训练也面临着一些挑战，其中之一是梯度消失或梯度爆炸的问题。当反向传播过程中的梯度变得非常小或非常大时，网络的参数更新会受到影响，导致训练变得困难。

梯度消失和梯度爆炸：

概念：

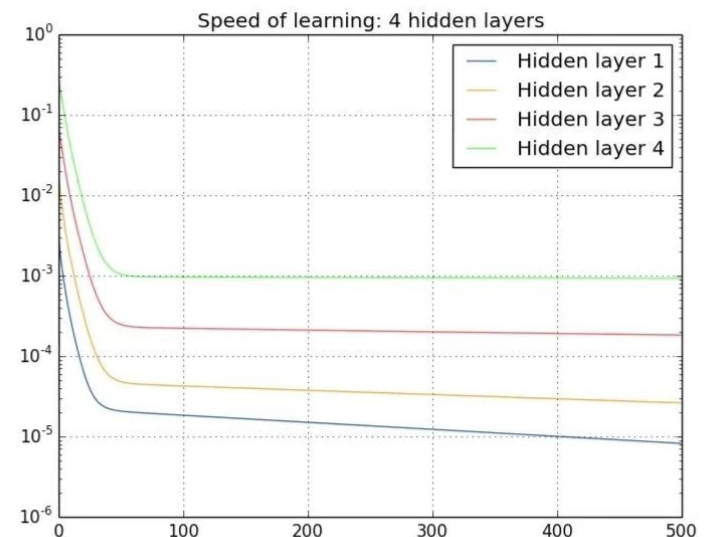
梯度消失：在深层网络中，梯度需要通过多个层次进行反向传播。根据链式法则，梯度在传播过程中会不断相乘，当层数较多时，梯度值可能会以指数形式衰减并趋近于零，导致梯度消失。

梯度爆炸：深层网络中的梯度在传播过程中也可能因链式法则的连乘效应而迅速增长，甚至呈指数级增长，导致网络参数更新过大，网络不稳定。

为什么会梯度消失：

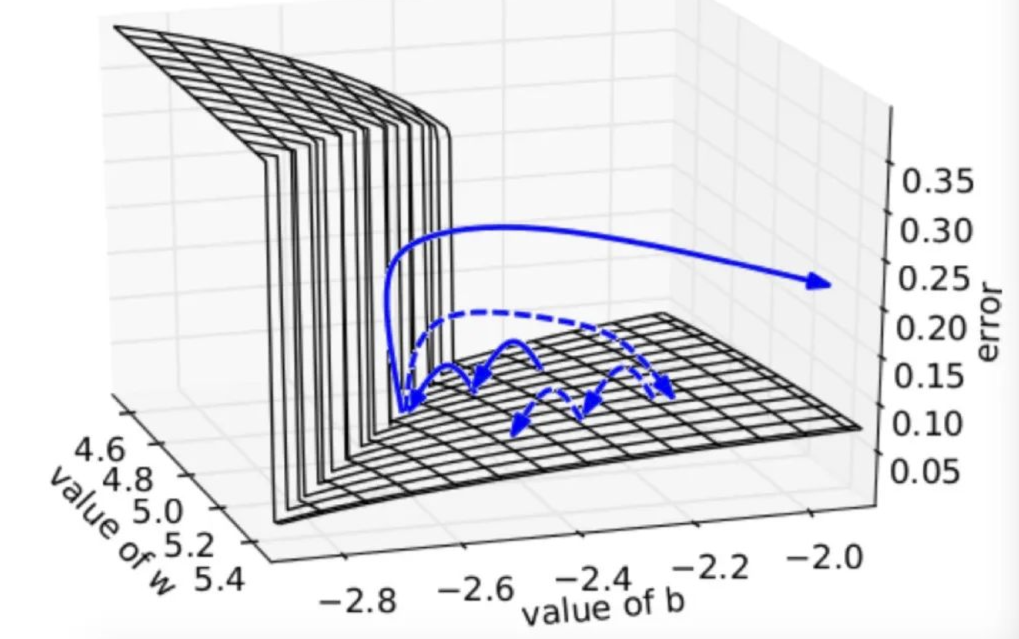
在使用激活函数为Sigmoid或Tanh等饱和激活函数时，因为这些函数在输入较大或较小的情况下会饱和并导致梯度变得非常小。当输入接近1时，Sigmoid函数的输出值会接近于1，导数趋近于0。于是在反向传播过程中，梯度的乘积会趋近于零。（为了缓解梯度消失问题，深度神经网络中常常使用其他类型的激活函数，如ReLU）

深度神经网络中，梯度是通过链式法则进行反向传播的。每一层的梯度都需要与前一层的梯度相乘，然后再传递到前一层，依此类推，直到传递到网络的输入层。如果网络层数较多，那么在反向传播过程中会经过多次连续的乘法操作，从而可能导致梯度的值指数级地减小，最终趋近于零，即梯度消失。
image-20240909211427431.png

为什么会梯度爆炸：

  • 神经网络经过多次的连乘，每次乘法操作都可能将梯度放大，从而导致梯度值变得非常大，从而导致梯度爆炸。

  • 梯度爆炸会导致网络的权重参数更新过大，从而使得模型的训练变得不稳定。

    image-20240909211523062.png

残差连接的思想：

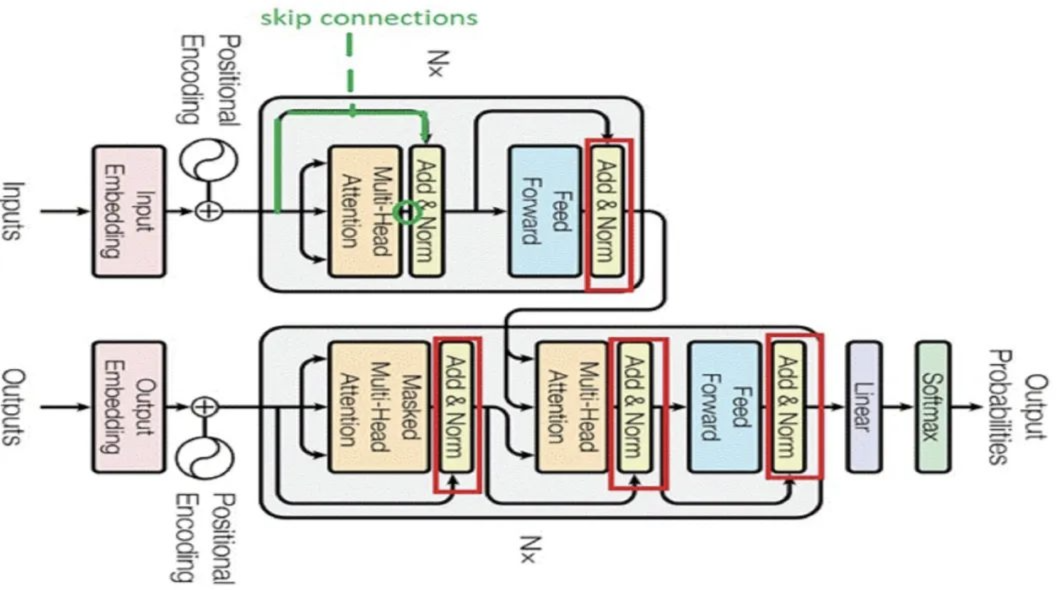
残差连接的核心思想是在网络的一层或多层之间引入直接连接，使得这些层的输出不仅包括经过非线性变换的特征，还包括未经处理的输入特征。这样做的目的是允许网络学习到的是输入和输出之间的残差（即差异），而不是直接学习一个完整的映射。这种方式有助于梯度在训练过程中更有效地回流，减轻深度网络中梯度消失的问题。

残差连接的核心思想是引入一个“快捷连接”（shortcut connection）或“跳过连接”（skip connection），允许数据绕过一些层直接传播。这样，网络中的一部分可以直接学习到输入与输出之间的残差（即差异），而不是直接学习到映射本身。具体来说，如果我们希望学习的目标映射是 H(x)，我们让网络学习残差映射 F(x)=H(x)−x。因此，原始的目标映射可以表示为 F(x)+x。

补一个跳过连接（skip connections）：

Skip connections的实现方式通常是将某一层的输出（通常经过一个恒等映射或简单的线性变换）直接加到下一层（或更深层）的输出上。 这样，网络的输出就可以表示为输入的非线性变换与输入的线性叠加，即y = F(x) + x，其中F(x)表示输入x经过一系列非线性变换后的输出，x表示直接传递的输入。
e.g. :

  • 模型一共56层，若第20层时模型已经充分学习达到测试集最佳效果，则让从21层开始到第56层学习一种恒等变换，在最后一层将第20层的输出恒等映射出来。

    image-20240909211034228.png

    残差连接是一种跳过连接。

具体实现：

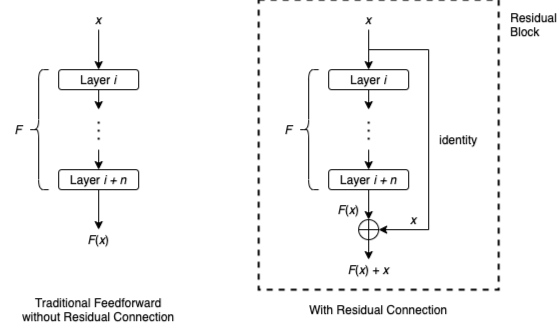
在传统的深度神经网络中，每一层的输出是基于前一层的输出进行计算。当网络层次增加时，网络的训练变得困难，因为梯度在反向传播过程中容易消失或爆炸。残差连接通过添加额外的“快捷连接”（shortcut connections）来解决这个问题。这些快捷连接允许一部分输入直接跳过一个或多个层传到更深的层，从而在不增加额外参数或计算复杂度的情况下，促进梯度的直接反向传播。

具体来说：设想一个简单的网络层，其输入为 𝑥，要通过一个非线性变换 𝐹(𝑥) 来得到输出。在没有残差连接的情况下，这个层的输出就是 𝐹(𝑥)。当引入残差连接后，这个层的输出变为𝐹(𝑥) + 𝑥。这里的𝑥是直接从输入到输出的跳过连接（Skip Connection），𝐹(𝑥) + 𝑥即是考虑了输入本身的残差输出。这样设计允许网络在需要时倾向于学习更简单的函数（例如，当 𝐹(𝑥) 接近0时，输出接近输入），这有助于提高网络的训练速度和准确性。

优点：

  1. 梯度传播： 梯度能够更容易地通过残差连接传递。在反向传播时，由于直接的跳过连接，梯度不会消失得太快，使得训练更加容易。

  2. 信息流动： 残差连接允许信息直接从输入层流向后续层，减轻了深度网络中信息难以传递的问题，有助于保持更加直接的信息流动。

  3. 网络深度： 允许构建非常深的网络而不会遇到梯度消失的问题，从而推动了深度学习模型的发展。

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    44
    45
    46
    47
    48
    49
    50
    51
    52
    53
    54
    55
    56
    57
    58
    59
    60
    61
    62
    63
    64
    65
    66
    67
    68
    69
    70
    71
    72
    73
    74
    75
    76
    77
    78
    79
    80
    81
    82
    83
    84
    85
    86
    87
    88
    89
    90
    91
    92
    93
    94
    95
    96
    97
    98
    99
    100
    101
    import torch
    import torch.nn as nn
    import torch.nn.functional as F
     
    # 定义残差块
    class ResidualBlock(nn.Module):
        def __init__(self, in_channels, out_channels, stride=1):
            super(ResidualBlock, self).__init__()
     
            # 第一个卷积层
            self.conv1 = nn.Conv2d(in_channels, out_channels, kernel_size=3, stride=stride, padding=1, bias=False)
            self.bn1 = nn.BatchNorm2d(out_channels)
     
            # 激活函数
            self.relu = nn.ReLU(inplace=True)
     
            # 第二个卷积层
            self.conv2 = nn.Conv2d(out_channels, out_channels, kernel_size=3, stride=1, padding=1, bias=False)
            self.bn2 = nn.BatchNorm2d(out_channels)
     
            # 如果输入和输出的通道数不一致，需要进行调整，用于残差连接
            self.shortcut = nn.Sequential()
            if stride != 1 or in_channels != out_channels:
                self.shortcut = nn.Sequential(
                    nn.Conv2d(in_channels, out_channels, kernel_size=1, stride=stride, bias=False),
                    nn.BatchNorm2d(out_channels)
                )
     
        def forward(self, x):
            residual = x  # 保存输入，用于残差连接
     
            # 第一个卷积块
            out = self.conv1(x)
            out = self.bn1(out)
            out = self.relu(out)
     
            # 第二个卷积块
            out = self.conv2(out)
            out = self.bn2(out)
     
            out += self.shortcut(residual)  # 残差连接
            out = self.relu(out)
     
            return out
     
    # 定义ResNet模型
    class ResNet(nn.Module):
        def __init__(self, block, layers, num_classes=10):
            super(ResNet, self).__init__()
            self.in_channels = 64  # 输入通道数
            self.conv1 = nn.Conv2d(3, 64, kernel_size=3, stride=1, padding=1, bias=False)
            self.bn1 = nn.BatchNorm2d(64)
            self.relu = nn.ReLU(inplace=True)
     
            # 通过make_layer函数构建ResNet的各层
            self.layer1 = self.make_layer(block, 64, layers[0], stride=1)
            self.layer2 = self.make_layer(block, 128, layers[1], stride=2)
            self.layer3 = self.make_layer(block, 256, layers[2], stride=2)
            self.layer4 = self.make_layer(block, 512, layers[3], stride=2)
     
            # 全局平均池化层
            self.avg_pool = nn.AdaptiveAvgPool2d((1, 1))
     
            # 全连接层
            self.fc = nn.Linear(512, num_classes)
     
        # 构建每一层的函数
        def make_layer(self, block, out_channels, blocks, stride):
            layers = []
            layers.append(block(self.in_channels, out_channels, stride))
            self.in_channels = out_channels
            for _ in range(1, blocks):
                layers.append(block(out_channels, out_channels, stride=1))
            return nn.Sequential(*layers)
     
        def forward(self, x):
            # 第一个卷积块
            out = self.conv1(x)
            out = self.bn1(out)
            out = self.relu(out)
     
            # 后续各层的卷积块
            out = self.layer1(out)
            out = self.layer2(out)
            out = self.layer3(out)
            out = self.layer4(out)
     
            # 全局平均池化
            out = self.avg_pool(out)
            out = out.view(out.size(0), -1)
     
            # 全连接层
            out = self.fc(out)
     
            return out
     
    # 创建ResNet18模型
    model = ResNet(ResidualBlock, [2, 2, 2, 2])
     
    # 打印模型结构
    print(model)